前言
最近做推荐,召回其中的一个策略是采用协同过滤的算法,本来觉得不就是简单的一通计算相似度取topK相似用户做推荐就好嘛!但是真正做起来就要踩“大数据”的坑。
传统的基于协同过滤,核心在于计算相似度找到topK相似用户/物品,无论哪种计算相似度的时间复杂度都会随着用户/物品规模的扩大而呈平方增长,对于实际应用中,用户/物品往往达到千万甚至更多,因此暴力计算相似度显然不可行,这时就需要采用近似计算的方法,损失一部分精度来换取计算的效率。
最开始准备采用Facebook的Faiss框架来计算相似度,但是由于准备用go做服务,Faiss没有官方提供go的接口需要手动编译,而且计算用户相似度时,数据是动态的,用起来不那么方便,因此弃用Faiss转向LSH来计算用户的相似度。下面详述Min hashing和LSH(local sensitive hashing)原理。
Hash Functions
大家应该经常能听到哈希,也用过java类或相似的包来计算哈希值,哈希函数根据hash-key可以产生一个bucket number作为其存储位置,因此可以快速查询。hash table就是根据key-value通过hash function(记为h)得到映射的值进行寻址直接访问的数据结构。
- 对于不同的key得到同样的散列地址,即$k_{1}≠ k_{2}$但$h_{1} = h_{2}$,我们称之为碰撞。
- 若对于所有的key经过hash function的映射到每一个地址的概率是相等的,则成为均匀散列函数。
Min Hashing
Jaccard相似度
Jaccard index用于计算相似度,是距离的一种度量方式,假设有向量$S_{1}$和$S_{2}$,我们定义
Minhash
Min Hashing是LSH的一种,可以用于快速估计两个向量的相似度。Min Hashing和Jaccard相似度有很大的关系:
对两个向量进行Min Hashing,产生的哈希值相同的概率等于两个向量的Jaccard相似度
-- (1)
通过MinHash得到映射分两步:
- 首先对row进行permutation,每个向量做同样的操作
- 向量的MinHash值对应permutation后,取值为非零的第一行的row index
考虑为什么通过Minhash可以达到上述(1)所说的效果呢?我们举例如下,有四个向量,每个向量有5行(维)(我们可以把列看作User,行看作Item,即User$S_{1}$购买过2,3商品…):
表1:
| row | $S_{1}$ | $S_{2}$ | $S_{3}$ | $S_{4}$ |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 1 | 0 | 1 | 1 |
| 4 | 0 | 0 | 1 | 0 |
我们看$S_{1}$和$S_{2}$,每一行的取值分三种情况:
- $S_{1}$和$S_{2}$同为1
- $S_{1}$和$S_{2}$一个为0一个为1
- $S_{1}$和$S_{2}$同为0
由于矩阵通常很稀疏(考虑实际中用户与购买物品的矩阵),因此大部分为情况3,但是1和2决定来Jaccard($S_{1}$,$S_{2}$)和$h\left(S_{1}\right)=h\left(S_{2}\right)$概率,假设情况1有x行,情况2有y行,则$\operatorname{Jaccard}\left(S_{1}, S_{2}\right)=\frac{x}{x+y}$(x相当于$S_{1} \cap S_{2}$,y相当于$S_{1} \cup S_{2}$),若Permutation是随机的,则$S_{1}$和$S_{2}$从上向下找第一个非零属于情况1的概括为$\frac{x}{x+y}$。
Min Hashing signatures
如何通过Min Hashing产生签名呢?
对向量做m次permutation(m一般为几百或更小,小于原向量长度n),每一次经过permutation得到minhash记为$h_{1}, h_{2}, \ldots, h_{m}$, 则向量获得的签名可以表示为:
对于一个高维度的向量进行permutation也是非常耗时的,因此可以随机选择m个哈希函数代替permutation。具体做法如下:
- 取m个针对row index的哈希函数$h_{1},h_{2}, \ldots, h_{m}$将原始0,1…n-1映射到0,1…n-1上
- 记Sig(i,c)为第c列在第i个哈希函数下的MinHash值,初始值记做$\infty$
- 对于每一行r
- 计算$h_{1}(r),h_{2}(r),\ldots,h_{m}(r)$
- 对于每列c:
- 如果c在r行取值为0,忽略
- 如果c在r行取值为1,则对$i=1,2,…,m$计算Sig(i,c) = Min(Sig(i,c),$h_{i}(r)$)
对表1所示数据,我们举例说明Min Hashing签名生成过程,假设我们选择两个哈希函数对row index生成MinHash,如下表2所示:$h_{1}(x) = x+1 \mod 5$, $h_{2}(x) = 3x+1 \mod 5$
| row | $S_{1}$ | $S_{2}$ | $S_{3}$ | $S_{4}$ | x+1 mod 5 | 3x+1 mod 5 |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 2 | 4 |
| 2 | 0 | 1 | 0 | 1 | 3 | 2 |
| 3 | 1 | 0 | 1 | 1 | 4 | 0 |
| 4 | 0 | 0 | 1 | 0 | 5 | 3 |
初始时,哈希签名如下:
| row | $S_{1}$ | $S_{2}$ | $S_{3}$ | $S_{4}$ |
|---|---|---|---|---|
| $h_{1}$ | $\infty$ | $\infty$ | $\infty$ | $\infty$ |
| $h_{2}$ | $\infty$ | $\infty$ | $\infty$ | $\infty$ |
对于第0行,只有$S_{1}$ 和$S_{4}$为非零,且$h_{1}$和$h_{2}$均为1,则当前签名矩阵变为
| row | $S_{1}$ | $S_{2}$ | $S_{3}$ | $S_{4}$ |
|---|---|---|---|---|
| $h_{1}$ | 1 | $\infty$ | $\infty$ | 1 |
| $h_{2}$ | 1 | $\infty$ | $\infty$ | 1 |
对于第1行,$S_{3}$为1,对于$h_{1}$和$h_{2}$为2和4,则签名矩阵变为:
| row | $S_{1}$ | $S_{2}$ | $S_{3}$ | $S_{4}$ |
|---|---|---|---|---|
| $h_{1}$ | 1 | $\infty$ | 2 | 1 |
| $h_{2}$ | 1 | $\infty$ | 4 | 1 |
继续至第2行,$S_{2}$ 和$S_{4}$为非零,对应$h_{1}$和$h_{2}为3和2,$S_{4}$目前的值均为1,小于$h_{1}$,$h_{2}$对应的3和2,则签名矩阵变为:
| row | $S_{1}$ | $S_{2}$ | $S_{3}$ | $S_{4}$ |
|---|---|---|---|---|
| $h_{1}$ | 1 | 3 | 2 | 1 |
| $h_{2}$ | 1 | 2 | 4 | 1 |
…
最后扫描完第4行,最后得到签名矩阵为:
| row | $S_{1}$ | $S_{2}$ | $S_{3}$ | $S_{4}$ |
|---|---|---|---|---|
| $h_{1}$ | 1 | 3 | 0 | 1 |
| $h_{2}$ | 0 | 2 | 0 | 0 |
通过上述过程可以看到,实际的$Jaccard(S_{1},S_{4})=2/3$,但通过签名计算得到的$Jaccard(S_{1},S_{4})=1$,上述结果是由于示例只选择了两个哈希函数,在实际应用中,会选择更多的哈希函数并且向量数往往在百万千万级,这时就会比较相近了。
Local Sensitive Hashing(LSH)
经过Min Hashing,我们可以实现数据降维并保证降维后的数据保持原空间的相似度,降低了在物品维度很高时计算相似度的时间复杂度,但是当用户数巨大时,计算两两相似度仍旧需要很高的时间开销,如何进一步降低寻找相似用户的复杂度,就需要LSH这样一个近似算法来实现。
LSH常见的做法是经过多次哈希将相似的向量散列到相同的桶中,检索时,我们只需要考虑相同桶中的任意对作为候选集即可。我们称不相似的向量被散列到相同的桶样本为false positive,相似的向量被散列到不同到桶中的样本称为false negetive。
在有来Min Hashing签名的基础上,一个有效的办法是将签名分段,我们称之为band。如下图所示: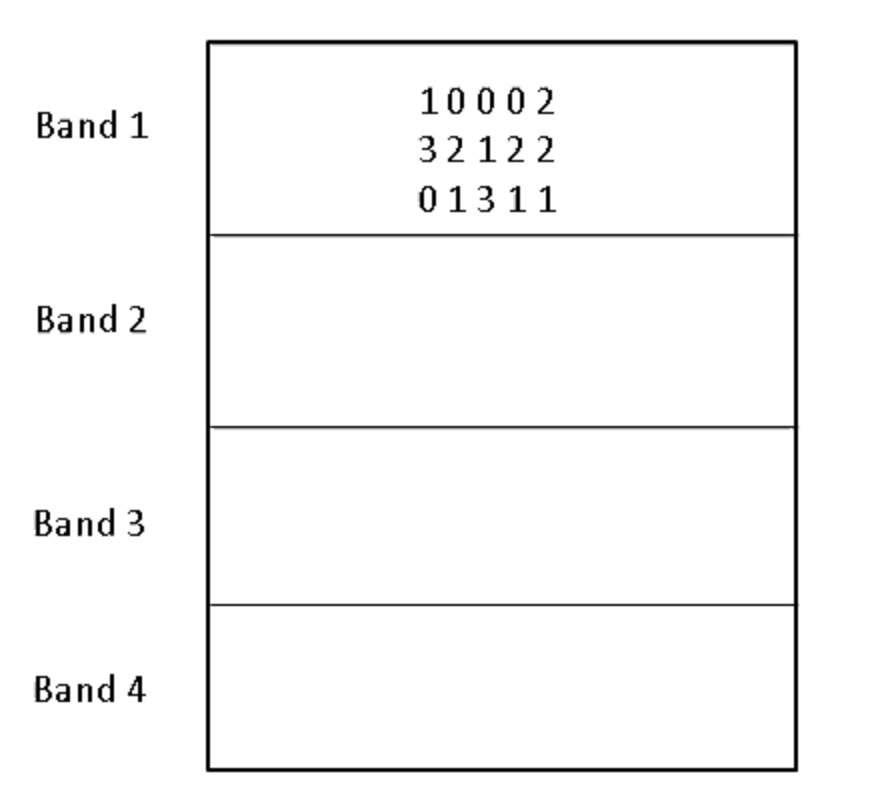
每个签名都被分成4段,向量的签名散列到对应的band上,如果band相同的越多,则其相似度越高。我们可以通过band获取candidate,计算candidate相似用户的相似度就好了。
如何选择band数?
假设我们有b和band,每个band有r行,即总的Min Hashing签名长度为b*r,假设两个向量的Jaccard相似度为s,则:
- 对于某一个band,所有行都相等的概率为:$s^r$
- 对于某一个band,至少有一行不同的概率为:$1 - s^r$
- 对所有band,至少有一行不同的概率为: $(1 - s^r)^b$
- 至少有一个band的所有行都相等的概率为: $1- (1 - s^r)^b$,即两个用户成为candidate的概率
上述概率在r,b不同值时为一个S曲线,如当r=6,b=100时的曲线如下图:
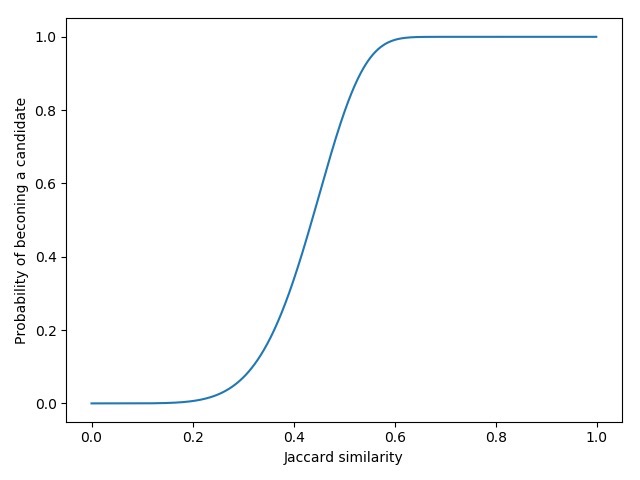
我们定义超过0.5的概率就有可能成为candidate,此时对应的相似度称为threshold:
在实际应用中,我们需要先确定最小相似度,即相似度大于多少我们认为可以作为candidate,然后确定哈希签名的长度进而可以确定b和r。我们需要考虑的是:
- 我们想要尽可能少出现false negative,我们需要选择b和r使得thresh< 我们定义的最小相似度。
- 如果要保证计算速度快并尽可能少出现false positive,我们需要选择b和r使得thresh>最小相似度。
参考文献:
- Mining of massive datasets; Jeffrey D. Ullman Anand Rajaraman, Jure Leskovec.
- 大规模数据的相似度计算:LSH算法