FM
FM常用于CTR估计,能够处理稀疏数据下的特征组合的问题。
FM原理
一般的线性模型不考虑特征之间的关系,公式定义如下:
为了表达特征之间的相关性,利用多项式函数,定义如下:
如上述公式,定义的二阶特征参数有$\frac{n*(n-1)}{2}$个,同时当特征非常稀疏且纬度高时,不仅时间复杂度在增加,同时由于稀疏的特征,很多二阶特征系数通常学习不到。
为了解决上述的问题,FM对每个特征引入辅助向量$V_{i} = [v_{i1},v_{i2},…v_{ik}]^{T}$,此时每个特征学习到一个k纬向量而不是一个值,从而解决数据稀疏下到特征组合问题。此时模型如下:
其中k表示辅助向量的纬度,为超参数。上述表达式的时间复杂度为$kn^{2}$。为降低时间复杂度,对(3)式最后一项做如下变化:
$\sum _ { i = 1 } ^ { n } \sum _ { j = i + 1 } ^ { n } < V _ { i } , V _ { j } > x _ { i } x _ { j }$
$= \frac { 1 } { 2 } \sum _ { i = 1 } ^ { n } \sum _ { j = 1 } ^ { n } < V _ { i } , V _ { j } > x _ { i } x _ { j } - \frac { 1 } { 2 } \sum _ { i = 1 } ^ { n } < V _ { i } , V _ { i } > x _ { i } x _ { i }$
$=\frac{1}{2}(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{k}v_{if}v_{jf}x_{i}x_{j} - \sum_{i=1}^{n}\sum_{f=1}^{k}v_{if}v_{if}x_ix_i)$
$=\frac{1}{2}\sum_{f=1}^{k}((\sum_{i=1}^{n}v_{if}x_{i})^2 - \sum_{i=1}^{n}(v_{if}x_i)^2)$
通过上述变化可以发现,将公式(3)的时间复杂度从$kn^{2}$降低为$kn$。
FM优点
- 通过引入辅助向量,能够解决稀疏数据的特征组合问题。
- 模型的时间复杂度为线性的(kn)。
FFM
FFM(Field-aware Factorization Machine)为FM的改进版,区别是FM的辅助向量为K维,而FFM的辅助向量为F*K维,其中F为field个数。对应的FFM模型如下:
其中$f_{i,f_{j}}$为i特征属于$f_{j}$下的辅助向量。由于FFM不能按照(3)进行化简,因此时间复杂度为$kn^{2}$。
FFM优缺点
- 与FM相比FFM具有field感知能力,模型能力更强。
- 与FM相比,辅助向量变为F*K维学习参数变为FM的F倍。
- 与FM相比,时间复杂度高。
DeepFM
由于FM/FFM使用的是一阶和二阶特征,为了学习更高阶特征,Huifeng Guo等人提出了DeepFM。
与DeepFM相似的模型有FNN,PNN,Wide&deep,模型结构如下图所示: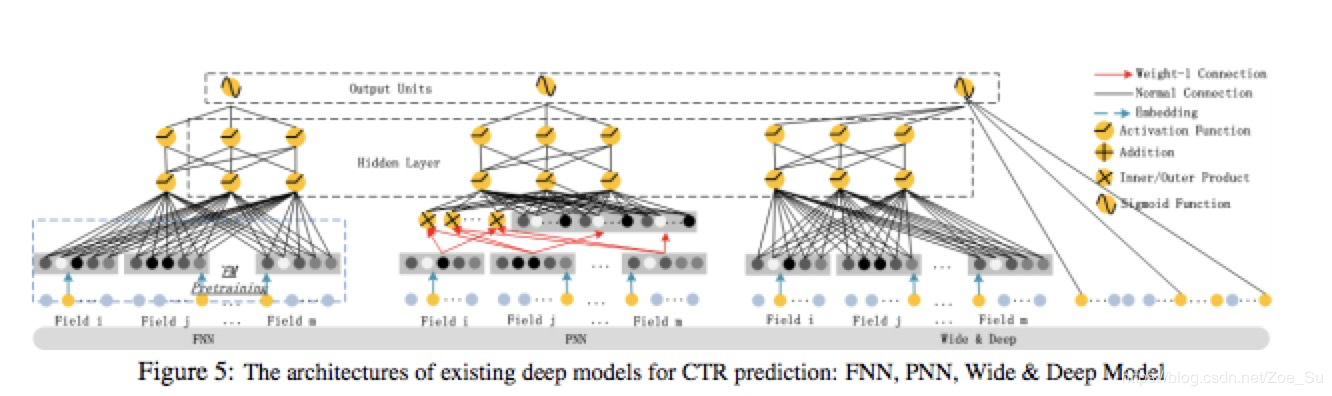
FNN使用预训练好的权重作为NN的输入,只能得到高阶特征组合,PNN则是在embedding层和第一层隐藏层中加入了product操作。Wide&deep 的提出则是为了综合低阶特征组合和高阶特征组合,wide部分多为专家经过特征工程得到的低阶组合特征,而deep部分则通过NN网络学习到高阶特征。
DeepFM不仅可以达到Wide&deep同时学习低阶特征组合和高阶特征组合的效果,同时想比于Wide&deep网络的优点是,不需要专家经过特征组合筛选特征。网络结果如下: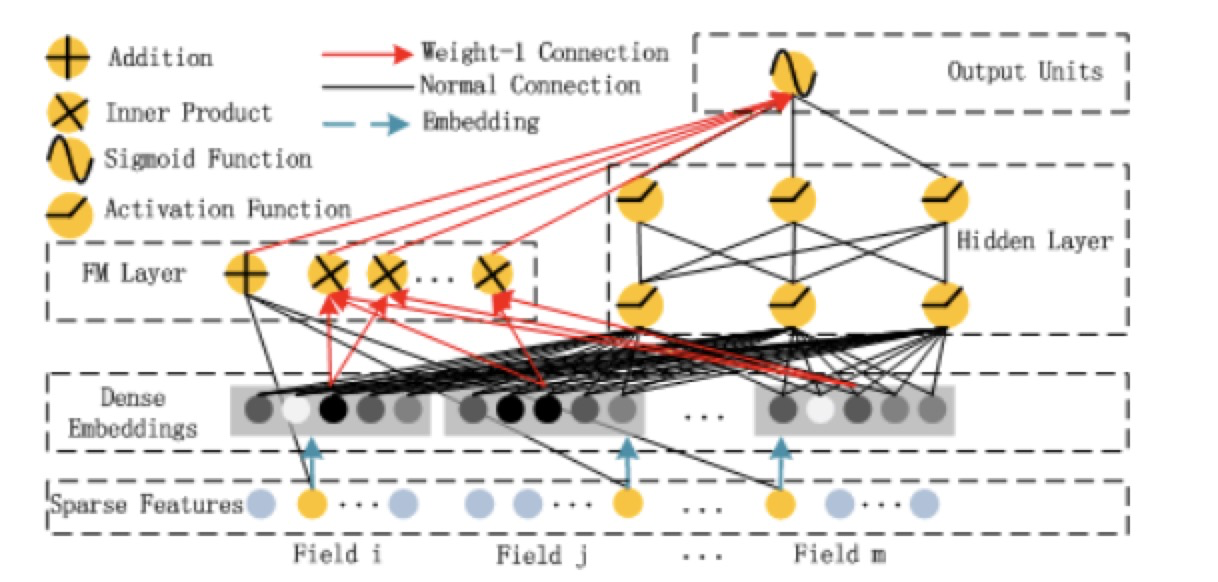
参考文献
- DeepFM: A Factorization-Machine based Neural Network for CTR Prediction [https://arxiv.org/pdf/1703.04247.pdf]
- 推荐系统召回四模型之:全能的FM模型
[https://zhuanlan.zhihu.com/p/58160982] - CTR预估算法之FM, FFM, DeepFM及实践
[https://blog.csdn.net/John_xyz/article/details/78933253]